Sidebar. Nucleons and electrons. Chemical bonds and nuclear binding
How are stars assembled from chemical elements, especially hydrogen and helium? How are chemical elements themselves composed of “elementary particles, the protons, neutrons, and electrons (and some evanescent particles)? What’s the state of the chemical elements inside the Sun or other stars? Of course, it depends upon the location within the star – the hot core (15 million kelvin) or the much cooler surface or photosphere (still very hot by our Earthly standards, at 5800K or about 10,000°F). If atomic and nuclear physics is not your bag, a review may help.
Structure of the atom and its nucleus:
Atoms consist of an extremely small and positively charged nucleus with negatively charged electrons circulating around them. A classic view was that the electrons ran in circular or elliptical orbits, but the modern quantum mechanical view is richer, as I summarize later in the main text. Electrons appear to be ultimately simple elementary particles with no internal structure (even though they have a magnetic moment as if electrical charge is circulating inside them!). Nuclei are composite goodies made of protons, each with a single positive charge of the exact same value as the charge of the electron, and uncharged neutrons. Both the proton and the neutron are heavy, over 1800 times as heavy as the electron. The only exception is ordinary hydrogen, whose nucleus is a single proton. It does have isotopes, stable deuterium or heavy hydrogen, with a proton and a neutron, and radioactively unstable tritium with a proton and two neutrons. Tritium is in hydrogen bombs and, less dramatically, in a few unpowered luminescent tubes.
The electromagnetic force holds the electrons around the nucleus, at a relatively great distance. A proton has a diameter of 0.83 femtometers or quadrillionths (10-15) meters. The mean distance of the electron in a single hydrogen atom is 53 picometers (pm), 53×10-12 m, which is about 64,000 times larger. Atoms under Earthly conditions are mostly empty space. Still, it’s hard to crush them together with Earthly forces. The electrical repulsion is very strong, and the quantum statistics of electrons works in, as two electrons can’t be pushed into the same state.
Molecules are held together by electromagnetic forces, constrained by quantum-mechanical laws that determine what distributions in space and in state of motion that the electrons can attain. The first molecule whose chemical binding was described by physical theory was, naturally, the hydrogen molecule, H2. Linus Pauling at Caltech carried out an approximate calculation that accounted for about 60% of the true energy of binding.
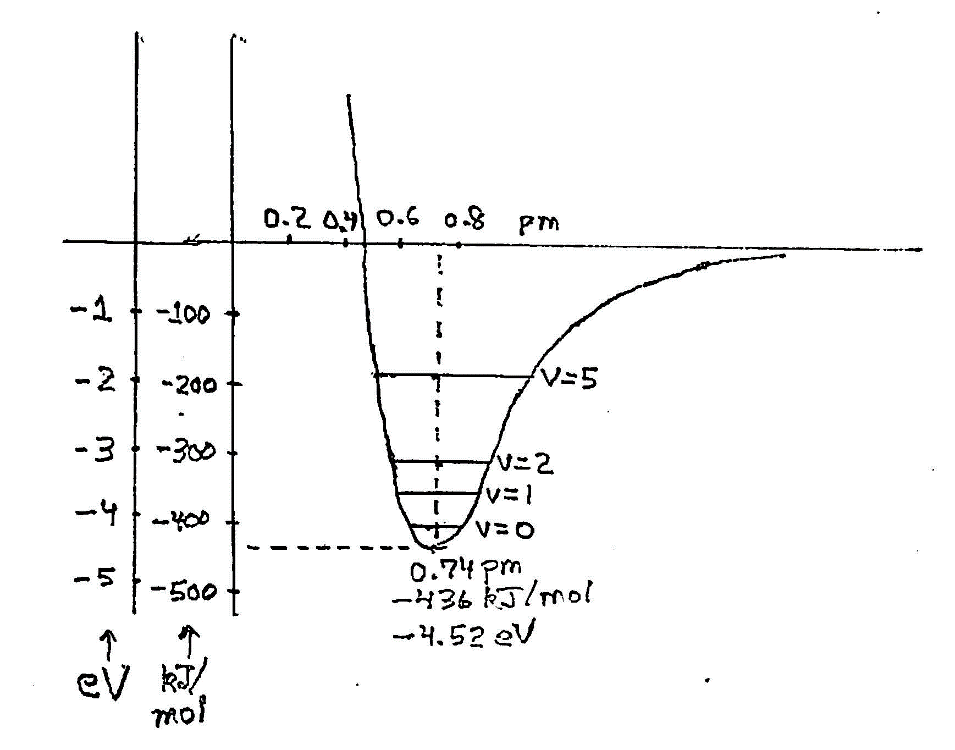Energy diagram for two hydrogen atoms in their lowest energy state. Relative to their free state when they are far apart, they are bound together with an energy as low as 436 kilojoules per mole at the “optimal” separation of 0.74 pm. This is only 70% of the sum of their nominal sizes as free atoms. They can move to and fro, and, in fact, in quantum mechanics they have a nonzero energy of vibration in their lowest possible state. That’s indicate by a vibrational quantum number v=0. There are other allowed stable states of vibration, v=1, v=2, and so on, with higher energies.
The bonding energy is perhaps comprehended more readily in macroscopic terms as 436,000 joules per mole, with a mole of H2 being 2.016 grams. That’s 1/8th of a kilowatt-hour. It takes a lot of energy and a high temperature to dissociate it back to neutral hydrogen atoms, plain H. The temperature can be calculated using the relation that individual entities such as single molecules have an average energy equal to kT at any temperature, T. Here, k is Boltzmann’s constant, 138×10-2 joules per kelvin. Equating that to the dissociation energy gives us a temperature of 52,400K (kelvin), 93,900°F, or almost 10 times the temperature of the Sun’s surface (outer layer, or photosphere) at 5800K. At that temperature about 2/3 of the molecules are dissociated. That’s a strong bond, clearly.
The attractive strong force (great name) holds the protons and neutrons together in the nucleus, counterbalancing the repulsive electrical forces among all the protons. It is about 137 times stronger than the electromagnetic force, though it acts only to very short distances… roughly the separations of femtometers or less among the nucleons (nucleon = either proton or neutron). In assembling, say, a deuterium nucleus from one proton and one neutron, the energy release is massive. This is noted shortly in the main text. One can make comparisons with chemical reactions on a per mass basis, with nuclear binding energies being on the order of 100,000 times larger than chemical binding energies. This is naturally essential in the “operation” of the Sun and of other stars. The strong force acts through evanescent particles, mesons, exchanged among the nucleons. (It gets deeper, with nucleons being composed of quarks held together by gluons. We need not concern ourselves with that level of structural detail to comprehend the Sun’s energy and structure.)
The state of matter in the Sun varies greatly with depth. Near the surface at a nice, hot 5800K, hydrogen is surprisingly bound mostly into H2 molecules. The temperature is far too low to break up the molecules. Oddly, H2 was initially hard to detect its presence in the Sun because it interacts weakly with light.
Of course, temperatures increase with depth in the Sun. The profile of this increase is explained by the balance of forces, gravity against hydrostatic pressure. The H2 dissociation temperature is reached about 2% of the way inward toward the core. At yet higher energies (and corresponding temperatures) the electron of the H atom is kicked into higher states but still bound to the proton. The first excited state lies at an energy commonly expressed in electron volts as 10.2 eV, a bit more than twice the energy of breaking up H2 into 2 H atoms. A further dissociation occurs at yet higher temperatures, with the separation of the electron from the proton. That makes a new state of matter called a plasma. The protons move in a sea of electrons. The energy for this ionization of hydrogen is 13.6 eV, corresponding to a temperature of 158,000K or 284,000°F. That temperature is reached not much further into the Sun, about 4% inward. So, most of the Sun is a giant plasma ball. It gets very dense at the core, 160 times the density of water. Still, the protons are pretty widely spaced, at an average of 22,000 femtometers or nearly 27,000 times the radius of each proton. The Sun is hot and dense but mashing protons together to cause then to fuse into deuterium as the first step in its main energy cycle is a rare event. The average proton in the Sun lasts 9 billion years. To get really dense you need neutrons to abut each other in a neutron star. The density is 4×1017 kg m-3, or 2 billion metric tonnes in a teaspoon. That’s 200 times the mass of all the pyramids at Giza.
A note about heavier nuclei than hydrogen and deuterium: heavier elements with many protons are stabilized against the mutual electrical repulsion of the protons by the strong force using more and more of the uncharged neutrons. Selected stable elements and their p and n counts at lowest n content are:
* Bismuth, as in Pepto-Bismol, is actually very, very weakly radioactive, far, far less than natural potassium. It has a half-life, more than a billion times the age of the Universe.
There are no stable isotopes of technetium, element 43, nor of promethium, element 61, even though elements on both sides of them are stable.
Elements with too-low or too-high numbers of neutrons decay radioactively. Carbon-11 is one low on neutrons. It decays be kicking out a positive electron or positron, becoming stable boron-11 as a proton becomes effectively a neutron. Famous carbon-14 decays by kicking out an electron, thus changing a neutron into a proton and becoming stable nitrogen-14. Very heavy elements have two additional decay modes. One is alpha-decay, emitting a helium nucleus or alpha particle, two protons and a neutron. The other is fission. Uranium-235 undergoes very slow spontaneous fission to a variety of products, when by itself. Fission is the natural decay of only 2 atoms of 238U in 10 million, all the rest being by alpha decay. 3In reactors and bombs its decay accelerates as one atom catches the extra neutron of a self-destructed comrade. Many radioactive decays are accompanied by emission of an intensely energetic gamma ray, of much shorter wavelength than even X-rays.
Of course, in the Sun and other stars the primary interest is fusion, the reverse of fission. That’s the topic in the main text, shortly.